It is well-known that profitable options trading must be directional; either along with underlying security by the forecasting of its future move, or directionally by implied volatility via forecasting of its dynamics (to be more correct, by predicting the discrepancy between the implied and realized volatility). Theoretically, one factor can be isolated from another by either delta or vega hedging.
In the OptionSmile methodology of the options pricing, we use empirical distribution of underlying returns as a probability measure to find the Fair Value of a contract. Then, by comparing these values with the real market prices, we draw a conclusion about market mispricing. It is obvious that this difference between the two prices consists of both directional factors—underlying security move—and implied volatility of options.
In this post, we are going to present a method to eliminate the underlying price change factor (drift) to the Fair Value of options and to calculate the Driftless Fair Value of options.
This value is calculated by the same formulas as a normal Fair Value, but with eliminating a drift from the underlying returns distribution. Here is the graphical representation if this idea:
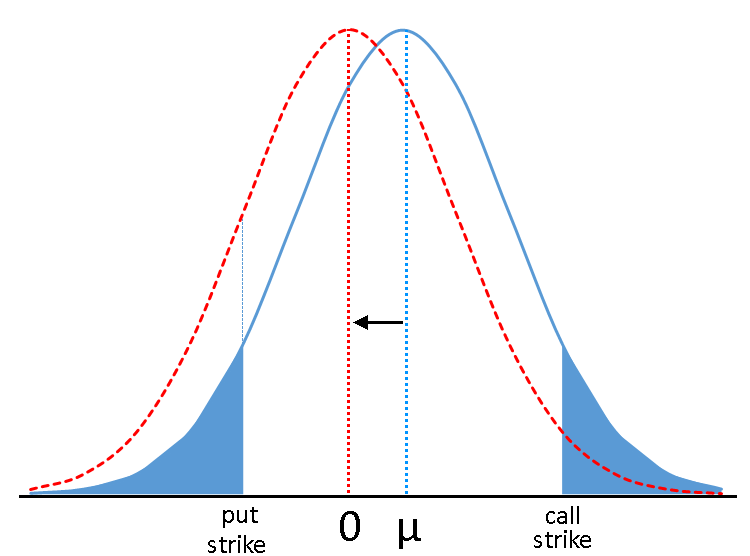
If we subtract this drift from each of the returns in our historical data set, we get another distribution (red dashed line) with the same shape but with a mean value equal zero, e.g., without a directional factor. This shift inevitably influences the Fair Values of our two options: put contract becomes more expensive because the area (probabilty density) on the left of its strike increases, while calls value decreases along with the area on the right side. After that, we can recalculate the Fair Values of our option contracts on the basis of this new measure—the new driftless distribution of underlying returns.
In the OptionSmile platform, the Driftless Fair Value series can be added to the Mispricing Chart by selecting the checkbox “Include DRIFTLESS Fair Value” on the Control Panel:
![]()
Here is the result of the Driftless Fair Value calculation for 20-days put options on SPY for the period of 1993 to 2017:
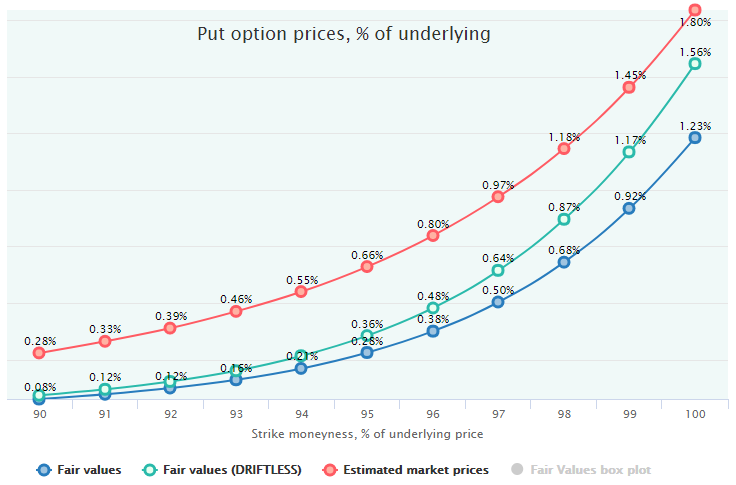
Notice one more line of the Fair Values calculated on the driftless distribution (green line). It has actually divided the whole area of a mispricing between blue (Fair Values) and red (market prices) lines. That provides an opportunity to estimate the input of each of the factors to the whole market mispricing:
Theoretically, the first, directional factor can be eliminated by delta-hedging, which makes the whole position delta neutral and independent from the underlying prices move. Such a portfolio would derive a return only from the second factor of option pricing—overestimation of future volatility. Of course, this is somewhat theoretical due to the hedging error because of delta convexity (gamma); and, in practice, actual profit will be dependent on the rehedging intervals. Nevertheless, that overall concept is working and allows us to evaluate the input of both factors.
Another interesting observation from the example above is that the directional factor plays a less significant role for the OTM strikes and much more on the ATM strikes. If we add ITM area, we get another interesting result: the ITM options mispricing is almost completely attributed to the directional factor because the Driftless Fair Value line almost coincides with the market prices there:
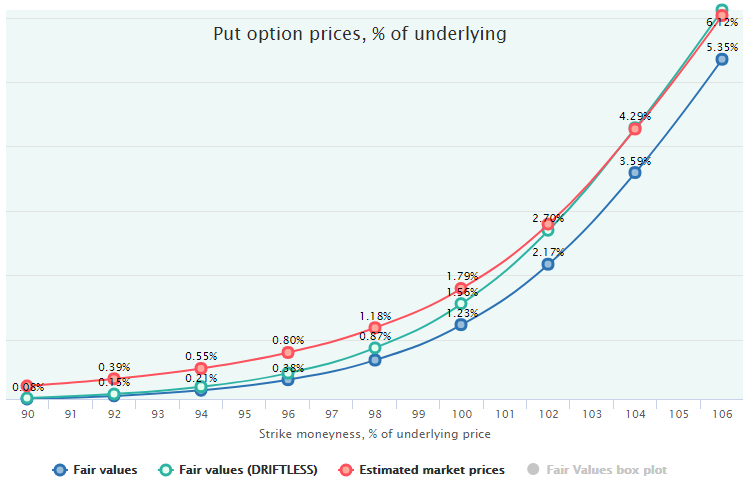
It is quite logical that the volatility factor is almost nonexistent is the upside strikes since buyers of equity options mostly seek a downside protection and are reluctant to overpay for the upside volatility.
It is interesting to repeat the same exercise with similar SPY call options (20 trading DTE) but take only the Bull Market of March 2009 – November 2017 (mean return is 1.38%, 17.4% annualized). Adding the Driftless Fair value to the chart reveals some interesting results.
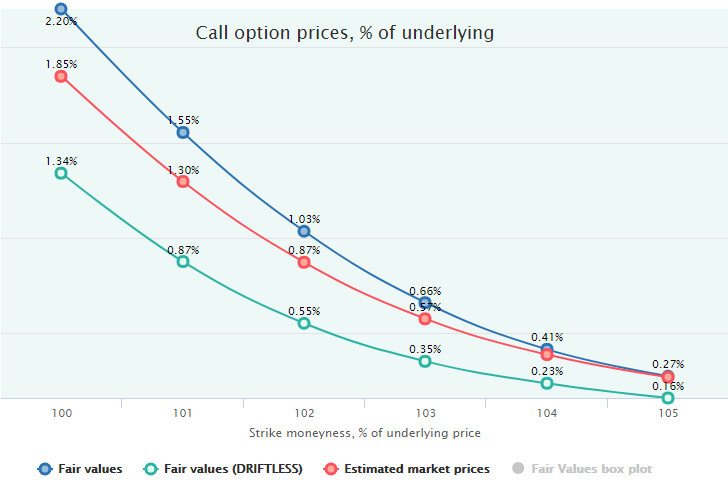
Due to the Bull Market, the call options have been underpriced in this period, and buying them would have been a profitable strategy. It turns out, this upward trend is the sole reason for the calls underpricing.
As we can see on this chart, the directional factor of underlying is very strong for calls: its elimination decreases the Fair Values significantly (green line) and places in below the Market Prices – outside of the total mispricing area. In this case, the factor of volatility overpricing works in the opposite direction and compensates some amount of the directional factor.
In other words, calls implied volatility is also overstated by the market despite their overall underpricing; perhaps, the demand for the puts protection also influences the right side of the volatility smile. However, selling these calls is a losing strategy due to the following strong upward move of underlying which completely eliminates this overpricing and makes these calls attractive for buying instead of selling.
It turns out that in such a market, it is profitable either to buy calls and participate in the upward move (although going against IV overpricing) or to sell them with delta-hedging and, hence, with directional factor removal and exploit the volatility overpricing factor only.
In many cases, the whole options mispricing can take place by only one factor, either a directional underlying move or a wrong estimation of probabilities by the options market.